mathworld.wolfram.com/DesarguesTheorem.html

Preview meta tags from the mathworld.wolfram.com website.

Linked Hostnames

5

Thumbnail

Search Engine Appearance

Google

https://mathworld.wolfram.com/DesarguesTheorem.html

Desargues' Theorem -- from Wolfram MathWorld

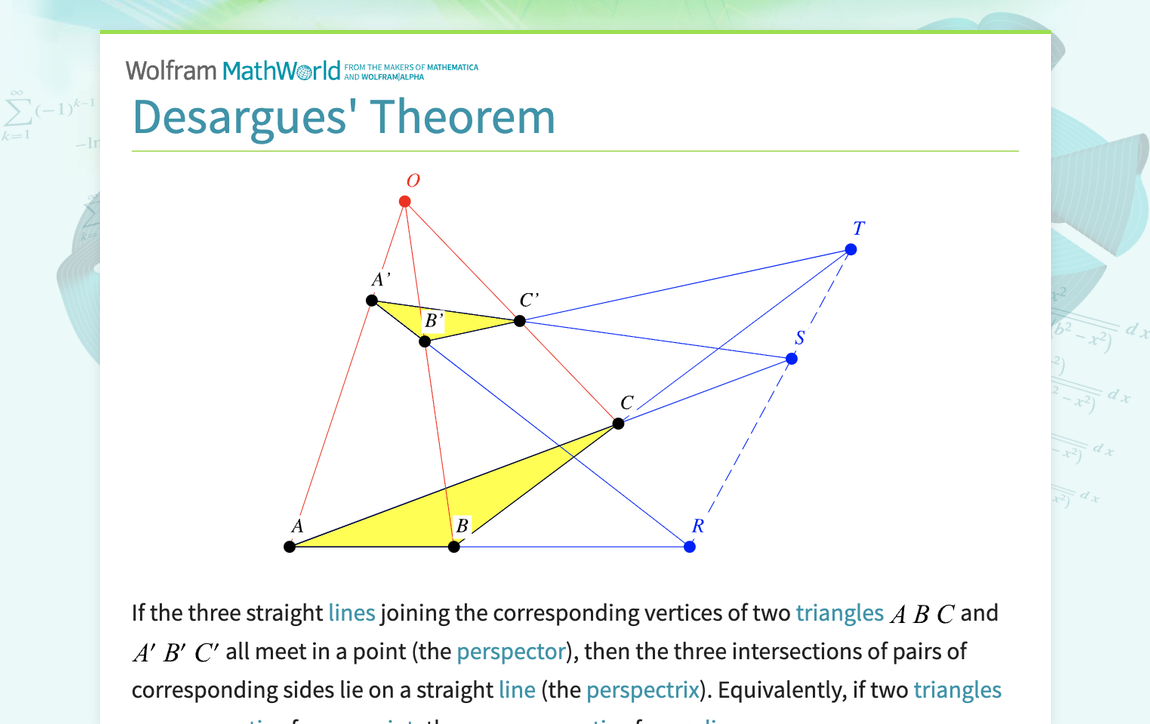
If the three straight lines joining the corresponding vertices of two triangles ABC and A^'B^'C^' all meet in a point (the perspector), then the three intersections of pairs of corresponding sides lie on a straight line (the perspectrix). Equivalently, if two triangles are perspective from a point, they are perspective from a line. The 10 lines and 10 3-line intersections form a 10_3 configuration sometimes called Desargues' configuration. Desargues' theorem is self-dual.



Bing

Desargues' Theorem -- from Wolfram MathWorld

https://mathworld.wolfram.com/DesarguesTheorem.html

If the three straight lines joining the corresponding vertices of two triangles ABC and A^'B^'C^' all meet in a point (the perspector), then the three intersections of pairs of corresponding sides lie on a straight line (the perspectrix). Equivalently, if two triangles are perspective from a point, they are perspective from a line. The 10 lines and 10 3-line intersections form a 10_3 configuration sometimes called Desargues' configuration. Desargues' theorem is self-dual.



DuckDuckGo

https://mathworld.wolfram.com/DesarguesTheorem.html

Desargues' Theorem -- from Wolfram MathWorld

If the three straight lines joining the corresponding vertices of two triangles ABC and A^'B^'C^' all meet in a point (the perspector), then the three intersections of pairs of corresponding sides lie on a straight line (the perspectrix). Equivalently, if two triangles are perspective from a point, they are perspective from a line. The 10 lines and 10 3-line intersections form a 10_3 configuration sometimes called Desargues' configuration. Desargues' theorem is self-dual.

  • General Meta Tags

    23
    • title
      Desargues' Theorem -- from Wolfram MathWorld
    • DC.Title
      Desargues' Theorem
    • DC.Creator
      Weisstein, Eric W.
    • DC.Description
      If the three straight lines joining the corresponding vertices of two triangles ABC and A^'B^'C^' all meet in a point (the perspector), then the three intersections of pairs of corresponding sides lie on a straight line (the perspectrix). Equivalently, if two triangles are perspective from a point, they are perspective from a line. The 10 lines and 10 3-line intersections form a 10_3 configuration sometimes called Desargues' configuration. Desargues' theorem is self-dual.
    • description
      If the three straight lines joining the corresponding vertices of two triangles ABC and A^'B^'C^' all meet in a point (the perspector), then the three intersections of pairs of corresponding sides lie on a straight line (the perspectrix). Equivalently, if two triangles are perspective from a point, they are perspective from a line. The 10 lines and 10 3-line intersections form a 10_3 configuration sometimes called Desargues' configuration. Desargues' theorem is self-dual.

  • Open Graph Meta Tags

    5
    • og:image
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_DesarguesTheorem.png
    • og:url
      https://mathworld.wolfram.com/DesarguesTheorem.html
    • og:type
      website
    • og:title
      Desargues' Theorem -- from Wolfram MathWorld
    • og:description
      If the three straight lines joining the corresponding vertices of two triangles ABC and A^'B^'C^' all meet in a point (the perspector), then the three intersections of pairs of corresponding sides lie on a straight line (the perspectrix). Equivalently, if two triangles are perspective from a point, they are perspective from a line. The 10 lines and 10 3-line intersections form a 10_3 configuration sometimes called Desargues' configuration. Desargues' theorem is self-dual.

  • Twitter Meta Tags

    5
    • twitter:card
      summary_large_image
    • twitter:site
      @WolframResearch
    • twitter:title
      Desargues' Theorem -- from Wolfram MathWorld
    • twitter:description
      If the three straight lines joining the corresponding vertices of two triangles ABC and A^'B^'C^' all meet in a point (the perspector), then the three intersections of pairs of corresponding sides lie on a straight line (the perspectrix). Equivalently, if two triangles are perspective from a point, they are perspective from a line. The 10 lines and 10 3-line intersections form a 10_3 configuration sometimes called Desargues' configuration. Desargues' theorem is self-dual.
    • twitter:image:src
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_DesarguesTheorem.png

  • Link Tags

    4
    • canonical
      https://mathworld.wolfram.com/DesarguesTheorem.html
    • preload
      //www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
    • stylesheet
      /css/styles.css
    • stylesheet
      /common/js/c2c/1.0/WolframC2CGui.css.en

Links

59