mathworld.wolfram.com/FibonacciNumber.html

Preview meta tags from the mathworld.wolfram.com website.

Linked Hostnames

23

Thumbnail

Search Engine Appearance

Google

https://mathworld.wolfram.com/FibonacciNumber.html

Fibonacci Number -- from Wolfram MathWorld

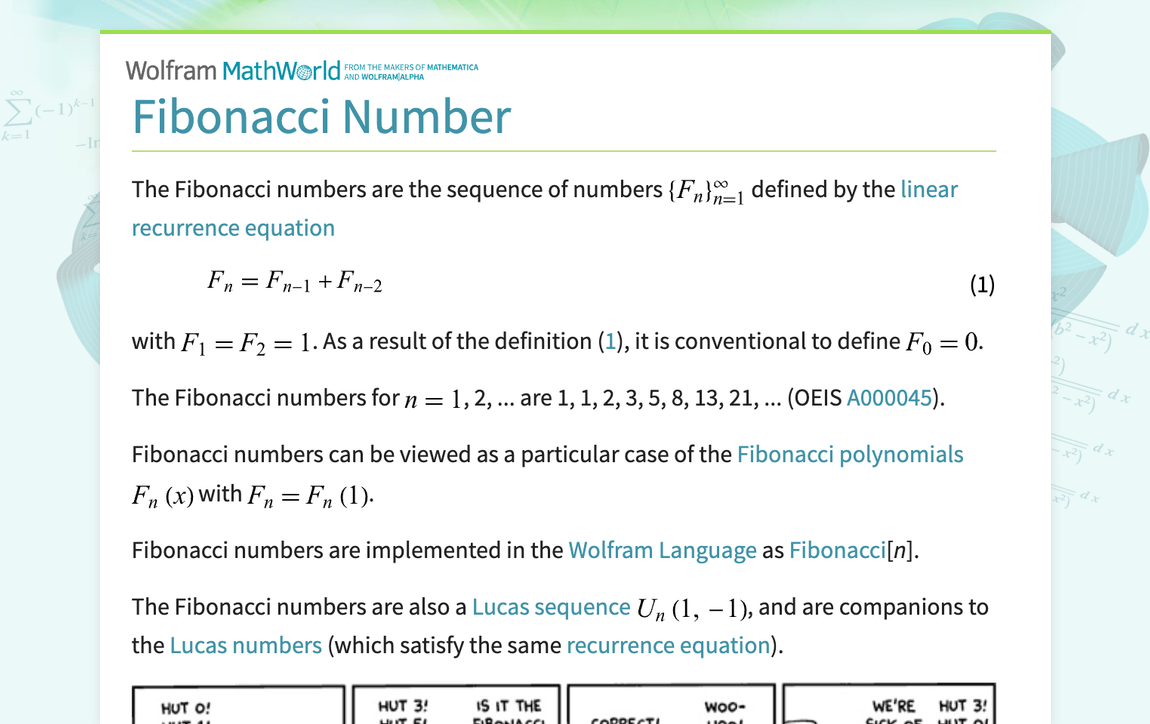
The Fibonacci numbers are the sequence of numbers {F_n}_(n=1)^infty defined by the linear recurrence equation F_n=F_(n-1)+F_(n-2) (1) with F_1=F_2=1. As a result of the definition (1), it is conventional to define F_0=0. The Fibonacci numbers for n=1, 2, ... are 1, 1, 2, 3, 5, 8, 13, 21, ... (OEIS A000045). Fibonacci numbers can be viewed as a particular case of the Fibonacci polynomials F_n(x) with F_n=F_n(1). Fibonacci numbers are implemented in the Wolfram Language as Fibonacci[n]....



Bing

Fibonacci Number -- from Wolfram MathWorld

https://mathworld.wolfram.com/FibonacciNumber.html

The Fibonacci numbers are the sequence of numbers {F_n}_(n=1)^infty defined by the linear recurrence equation F_n=F_(n-1)+F_(n-2) (1) with F_1=F_2=1. As a result of the definition (1), it is conventional to define F_0=0. The Fibonacci numbers for n=1, 2, ... are 1, 1, 2, 3, 5, 8, 13, 21, ... (OEIS A000045). Fibonacci numbers can be viewed as a particular case of the Fibonacci polynomials F_n(x) with F_n=F_n(1). Fibonacci numbers are implemented in the Wolfram Language as Fibonacci[n]....



DuckDuckGo

https://mathworld.wolfram.com/FibonacciNumber.html

Fibonacci Number -- from Wolfram MathWorld

The Fibonacci numbers are the sequence of numbers {F_n}_(n=1)^infty defined by the linear recurrence equation F_n=F_(n-1)+F_(n-2) (1) with F_1=F_2=1. As a result of the definition (1), it is conventional to define F_0=0. The Fibonacci numbers for n=1, 2, ... are 1, 1, 2, 3, 5, 8, 13, 21, ... (OEIS A000045). Fibonacci numbers can be viewed as a particular case of the Fibonacci polynomials F_n(x) with F_n=F_n(1). Fibonacci numbers are implemented in the Wolfram Language as Fibonacci[n]....

  • General Meta Tags

    58
    • title
      Fibonacci Number -- from Wolfram MathWorld
    • DC.Title
      Fibonacci Number
    • DC.Creator
      Weisstein, Eric W.
    • DC.Description
      The Fibonacci numbers are the sequence of numbers {F_n}_(n=1)^infty defined by the linear recurrence equation F_n=F_(n-1)+F_(n-2) (1) with F_1=F_2=1. As a result of the definition (1), it is conventional to define F_0=0. The Fibonacci numbers for n=1, 2, ... are 1, 1, 2, 3, 5, 8, 13, 21, ... (OEIS A000045). Fibonacci numbers can be viewed as a particular case of the Fibonacci polynomials F_n(x) with F_n=F_n(1). Fibonacci numbers are implemented in the Wolfram Language as Fibonacci[n]....
    • description
      The Fibonacci numbers are the sequence of numbers {F_n}_(n=1)^infty defined by the linear recurrence equation F_n=F_(n-1)+F_(n-2) (1) with F_1=F_2=1. As a result of the definition (1), it is conventional to define F_0=0. The Fibonacci numbers for n=1, 2, ... are 1, 1, 2, 3, 5, 8, 13, 21, ... (OEIS A000045). Fibonacci numbers can be viewed as a particular case of the Fibonacci polynomials F_n(x) with F_n=F_n(1). Fibonacci numbers are implemented in the Wolfram Language as Fibonacci[n]....

  • Open Graph Meta Tags

    5
    • og:image
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_FibonacciNumber.png
    • og:url
      https://mathworld.wolfram.com/FibonacciNumber.html
    • og:type
      website
    • og:title
      Fibonacci Number -- from Wolfram MathWorld
    • og:description
      The Fibonacci numbers are the sequence of numbers {F_n}_(n=1)^infty defined by the linear recurrence equation F_n=F_(n-1)+F_(n-2) (1) with F_1=F_2=1. As a result of the definition (1), it is conventional to define F_0=0. The Fibonacci numbers for n=1, 2, ... are 1, 1, 2, 3, 5, 8, 13, 21, ... (OEIS A000045). Fibonacci numbers can be viewed as a particular case of the Fibonacci polynomials F_n(x) with F_n=F_n(1). Fibonacci numbers are implemented in the Wolfram Language as Fibonacci[n]....

  • Twitter Meta Tags

    5
    • twitter:card
      summary_large_image
    • twitter:site
      @WolframResearch
    • twitter:title
      Fibonacci Number -- from Wolfram MathWorld
    • twitter:description
      The Fibonacci numbers are the sequence of numbers {F_n}_(n=1)^infty defined by the linear recurrence equation F_n=F_(n-1)+F_(n-2) (1) with F_1=F_2=1. As a result of the definition (1), it is conventional to define F_0=0. The Fibonacci numbers for n=1, 2, ... are 1, 1, 2, 3, 5, 8, 13, 21, ... (OEIS A000045). Fibonacci numbers can be viewed as a particular case of the Fibonacci polynomials F_n(x) with F_n=F_n(1). Fibonacci numbers are implemented in the Wolfram Language as Fibonacci[n]....
    • twitter:image:src
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_FibonacciNumber.png

  • Link Tags

    4
    • canonical
      https://mathworld.wolfram.com/FibonacciNumber.html
    • preload
      //www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
    • stylesheet
      /css/styles.css
    • stylesheet
      /common/js/c2c/1.0/WolframC2CGui.css.en

Links

207