mathworld.wolfram.com/GaussianFunction.html

Preview meta tags from the mathworld.wolfram.com website.

Linked Hostnames

6

Thumbnail

Search Engine Appearance

Google

https://mathworld.wolfram.com/GaussianFunction.html

Gaussian Function -- from Wolfram MathWorld

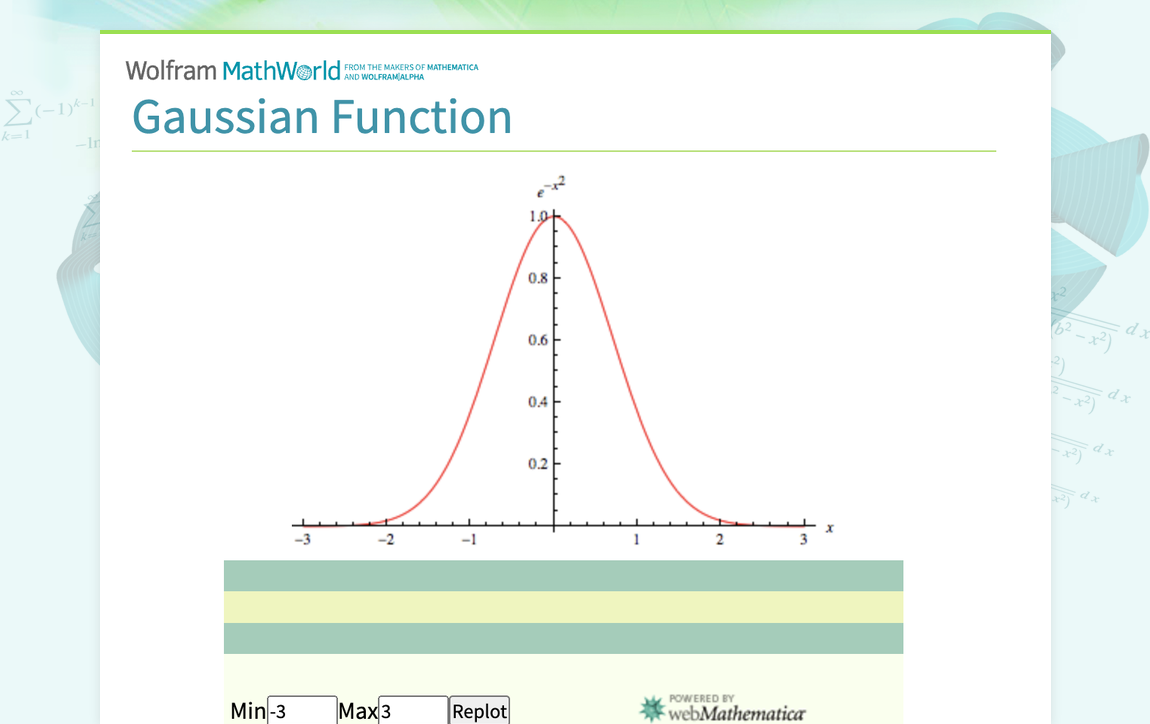
In one dimension, the Gaussian function is the probability density function of the normal distribution, f(x)=1/(sigmasqrt(2pi))e^(-(x-mu)^2/(2sigma^2)), (1) sometimes also called the frequency curve. The full width at half maximum (FWHM) for a Gaussian is found by finding the half-maximum points x_0. The constant scaling factor can be ignored, so we must solve e^(-(x_0-mu)^2/(2sigma^2))=1/2f(x_(max)) (2) But f(x_(max)) occurs at x_(max)=mu, so ...



Bing

Gaussian Function -- from Wolfram MathWorld

https://mathworld.wolfram.com/GaussianFunction.html

In one dimension, the Gaussian function is the probability density function of the normal distribution, f(x)=1/(sigmasqrt(2pi))e^(-(x-mu)^2/(2sigma^2)), (1) sometimes also called the frequency curve. The full width at half maximum (FWHM) for a Gaussian is found by finding the half-maximum points x_0. The constant scaling factor can be ignored, so we must solve e^(-(x_0-mu)^2/(2sigma^2))=1/2f(x_(max)) (2) But f(x_(max)) occurs at x_(max)=mu, so ...



DuckDuckGo

https://mathworld.wolfram.com/GaussianFunction.html

Gaussian Function -- from Wolfram MathWorld

In one dimension, the Gaussian function is the probability density function of the normal distribution, f(x)=1/(sigmasqrt(2pi))e^(-(x-mu)^2/(2sigma^2)), (1) sometimes also called the frequency curve. The full width at half maximum (FWHM) for a Gaussian is found by finding the half-maximum points x_0. The constant scaling factor can be ignored, so we must solve e^(-(x_0-mu)^2/(2sigma^2))=1/2f(x_(max)) (2) But f(x_(max)) occurs at x_(max)=mu, so ...

  • General Meta Tags

    24
    • title
      Gaussian Function -- from Wolfram MathWorld
    • DC.Title
      Gaussian Function
    • DC.Creator
      Weisstein, Eric W.
    • DC.Description
      In one dimension, the Gaussian function is the probability density function of the normal distribution, f(x)=1/(sigmasqrt(2pi))e^(-(x-mu)^2/(2sigma^2)), (1) sometimes also called the frequency curve. The full width at half maximum (FWHM) for a Gaussian is found by finding the half-maximum points x_0. The constant scaling factor can be ignored, so we must solve e^(-(x_0-mu)^2/(2sigma^2))=1/2f(x_(max)) (2) But f(x_(max)) occurs at x_(max)=mu, so ...
    • description
      In one dimension, the Gaussian function is the probability density function of the normal distribution, f(x)=1/(sigmasqrt(2pi))e^(-(x-mu)^2/(2sigma^2)), (1) sometimes also called the frequency curve. The full width at half maximum (FWHM) for a Gaussian is found by finding the half-maximum points x_0. The constant scaling factor can be ignored, so we must solve e^(-(x_0-mu)^2/(2sigma^2))=1/2f(x_(max)) (2) But f(x_(max)) occurs at x_(max)=mu, so ...

  • Open Graph Meta Tags

    5
    • og:image
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_GaussianFunction.png
    • og:url
      https://mathworld.wolfram.com/GaussianFunction.html
    • og:type
      website
    • og:title
      Gaussian Function -- from Wolfram MathWorld
    • og:description
      In one dimension, the Gaussian function is the probability density function of the normal distribution, f(x)=1/(sigmasqrt(2pi))e^(-(x-mu)^2/(2sigma^2)), (1) sometimes also called the frequency curve. The full width at half maximum (FWHM) for a Gaussian is found by finding the half-maximum points x_0. The constant scaling factor can be ignored, so we must solve e^(-(x_0-mu)^2/(2sigma^2))=1/2f(x_(max)) (2) But f(x_(max)) occurs at x_(max)=mu, so ...

  • Twitter Meta Tags

    5
    • twitter:card
      summary_large_image
    • twitter:site
      @WolframResearch
    • twitter:title
      Gaussian Function -- from Wolfram MathWorld
    • twitter:description
      In one dimension, the Gaussian function is the probability density function of the normal distribution, f(x)=1/(sigmasqrt(2pi))e^(-(x-mu)^2/(2sigma^2)), (1) sometimes also called the frequency curve. The full width at half maximum (FWHM) for a Gaussian is found by finding the half-maximum points x_0. The constant scaling factor can be ignored, so we must solve e^(-(x_0-mu)^2/(2sigma^2))=1/2f(x_(max)) (2) But f(x_(max)) occurs at x_(max)=mu, so ...
    • twitter:image:src
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_GaussianFunction.png

  • Link Tags

    4
    • canonical
      https://mathworld.wolfram.com/GaussianFunction.html
    • preload
      //www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
    • stylesheet
      /css/styles.css
    • stylesheet
      /common/js/c2c/1.0/WolframC2CGui.css.en

Links

53