mathworld.wolfram.com/Heap.html

Preview meta tags from the mathworld.wolfram.com website.

Linked Hostnames

6

Thumbnail

Search Engine Appearance

Google

https://mathworld.wolfram.com/Heap.html

Heap -- from Wolfram MathWorld

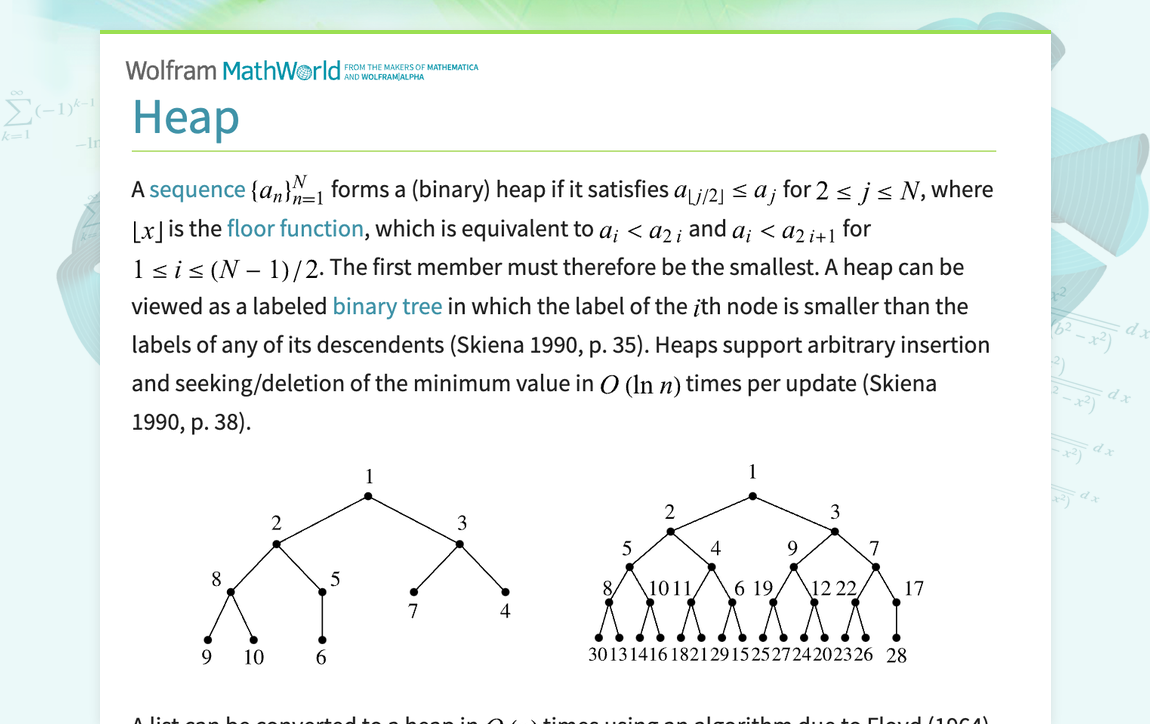
A sequence {a_n}_(n=1)^N forms a (binary) heap if it satisfies a_(|_j/2_|)<=a_j for 2<=j<=N, where |_x_| is the floor function, which is equivalent to a_i<a_(2i) and a_i<a_(2i+1) for 1<=i<=(N-1)/2. The first member must therefore be the smallest. A heap can be viewed as a labeled binary tree in which the label of the ith node is smaller than the labels of any of its descendents (Skiena 1990, p. 35). Heaps support arbitrary insertion and seeking/deletion of the minimum...



Bing

Heap -- from Wolfram MathWorld

https://mathworld.wolfram.com/Heap.html

A sequence {a_n}_(n=1)^N forms a (binary) heap if it satisfies a_(|_j/2_|)<=a_j for 2<=j<=N, where |_x_| is the floor function, which is equivalent to a_i<a_(2i) and a_i<a_(2i+1) for 1<=i<=(N-1)/2. The first member must therefore be the smallest. A heap can be viewed as a labeled binary tree in which the label of the ith node is smaller than the labels of any of its descendents (Skiena 1990, p. 35). Heaps support arbitrary insertion and seeking/deletion of the minimum...



DuckDuckGo

https://mathworld.wolfram.com/Heap.html

Heap -- from Wolfram MathWorld

A sequence {a_n}_(n=1)^N forms a (binary) heap if it satisfies a_(|_j/2_|)<=a_j for 2<=j<=N, where |_x_| is the floor function, which is equivalent to a_i<a_(2i) and a_i<a_(2i+1) for 1<=i<=(N-1)/2. The first member must therefore be the smallest. A heap can be viewed as a labeled binary tree in which the label of the ith node is smaller than the labels of any of its descendents (Skiena 1990, p. 35). Heaps support arbitrary insertion and seeking/deletion of the minimum...

  • General Meta Tags

    22
    • title
      Heap -- from Wolfram MathWorld
    • DC.Title
      Heap
    • DC.Creator
      Weisstein, Eric W.
    • DC.Description
      A sequence {a_n}_(n=1)^N forms a (binary) heap if it satisfies a_(|_j/2_|)<=a_j for 2<=j<=N, where |_x_| is the floor function, which is equivalent to a_i<a_(2i) and a_i<a_(2i+1) for 1<=i<=(N-1)/2. The first member must therefore be the smallest. A heap can be viewed as a labeled binary tree in which the label of the ith node is smaller than the labels of any of its descendents (Skiena 1990, p. 35). Heaps support arbitrary insertion and seeking/deletion of the minimum...
    • description
      A sequence {a_n}_(n=1)^N forms a (binary) heap if it satisfies a_(|_j/2_|)<=a_j for 2<=j<=N, where |_x_| is the floor function, which is equivalent to a_i<a_(2i) and a_i<a_(2i+1) for 1<=i<=(N-1)/2. The first member must therefore be the smallest. A heap can be viewed as a labeled binary tree in which the label of the ith node is smaller than the labels of any of its descendents (Skiena 1990, p. 35). Heaps support arbitrary insertion and seeking/deletion of the minimum...

  • Open Graph Meta Tags

    5
    • og:image
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_Heap.png
    • og:url
      https://mathworld.wolfram.com/Heap.html
    • og:type
      website
    • og:title
      Heap -- from Wolfram MathWorld
    • og:description
      A sequence {a_n}_(n=1)^N forms a (binary) heap if it satisfies a_(|_j/2_|)<=a_j for 2<=j<=N, where |_x_| is the floor function, which is equivalent to a_i<a_(2i) and a_i<a_(2i+1) for 1<=i<=(N-1)/2. The first member must therefore be the smallest. A heap can be viewed as a labeled binary tree in which the label of the ith node is smaller than the labels of any of its descendents (Skiena 1990, p. 35). Heaps support arbitrary insertion and seeking/deletion of the minimum...

  • Twitter Meta Tags

    5
    • twitter:card
      summary_large_image
    • twitter:site
      @WolframResearch
    • twitter:title
      Heap -- from Wolfram MathWorld
    • twitter:description
      A sequence {a_n}_(n=1)^N forms a (binary) heap if it satisfies a_(|_j/2_|)<=a_j for 2<=j<=N, where |_x_| is the floor function, which is equivalent to a_i<a_(2i) and a_i<a_(2i+1) for 1<=i<=(N-1)/2. The first member must therefore be the smallest. A heap can be viewed as a labeled binary tree in which the label of the ith node is smaller than the labels of any of its descendents (Skiena 1990, p. 35). Heaps support arbitrary insertion and seeking/deletion of the minimum...
    • twitter:image:src
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_Heap.png

  • Link Tags

    4
    • canonical
      https://mathworld.wolfram.com/Heap.html
    • preload
      //www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
    • stylesheet
      /css/styles.css
    • stylesheet
      /common/js/c2c/1.0/WolframC2CGui.css.en

Links

46