mathworld.wolfram.com/NumberFieldSieve.html

Preview meta tags from the mathworld.wolfram.com website.

Linked Hostnames

5

Thumbnail

Search Engine Appearance

Google

https://mathworld.wolfram.com/NumberFieldSieve.html

Number Field Sieve -- from Wolfram MathWorld

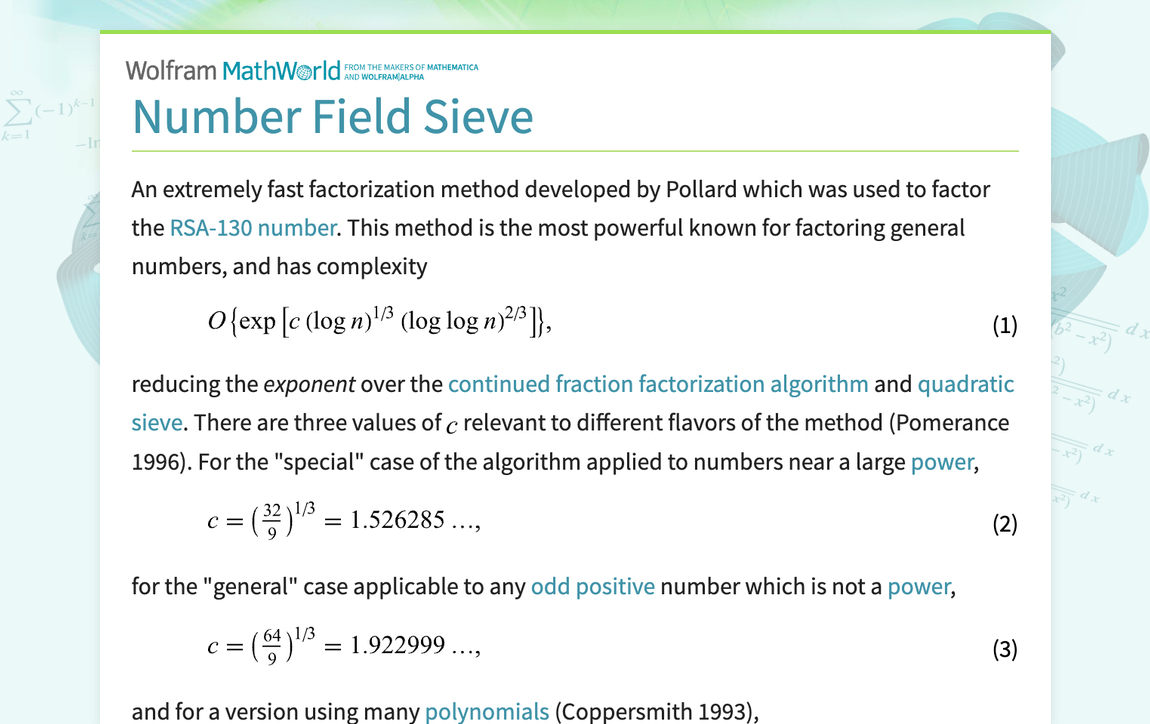
An extremely fast factorization method developed by Pollard which was used to factor the RSA-130 number. This method is the most powerful known for factoring general numbers, and has complexity O{exp[c(logn)^(1/3)(loglogn)^(2/3)]}, (1) reducing the exponent over the continued fraction factorization algorithm and quadratic sieve. There are three values of c relevant to different flavors of the method (Pomerance 1996). For the "special" case of the algorithm applied to numbers...



Bing

Number Field Sieve -- from Wolfram MathWorld

https://mathworld.wolfram.com/NumberFieldSieve.html

An extremely fast factorization method developed by Pollard which was used to factor the RSA-130 number. This method is the most powerful known for factoring general numbers, and has complexity O{exp[c(logn)^(1/3)(loglogn)^(2/3)]}, (1) reducing the exponent over the continued fraction factorization algorithm and quadratic sieve. There are three values of c relevant to different flavors of the method (Pomerance 1996). For the "special" case of the algorithm applied to numbers...



DuckDuckGo

https://mathworld.wolfram.com/NumberFieldSieve.html

Number Field Sieve -- from Wolfram MathWorld

An extremely fast factorization method developed by Pollard which was used to factor the RSA-130 number. This method is the most powerful known for factoring general numbers, and has complexity O{exp[c(logn)^(1/3)(loglogn)^(2/3)]}, (1) reducing the exponent over the continued fraction factorization algorithm and quadratic sieve. There are three values of c relevant to different flavors of the method (Pomerance 1996). For the "special" case of the algorithm applied to numbers...

  • General Meta Tags

    22
    • title
      Number Field Sieve -- from Wolfram MathWorld
    • DC.Title
      Number Field Sieve
    • DC.Creator
      Weisstein, Eric W.
    • DC.Description
      An extremely fast factorization method developed by Pollard which was used to factor the RSA-130 number. This method is the most powerful known for factoring general numbers, and has complexity O{exp[c(logn)^(1/3)(loglogn)^(2/3)]}, (1) reducing the exponent over the continued fraction factorization algorithm and quadratic sieve. There are three values of c relevant to different flavors of the method (Pomerance 1996). For the "special" case of the algorithm applied to numbers...
    • description
      An extremely fast factorization method developed by Pollard which was used to factor the RSA-130 number. This method is the most powerful known for factoring general numbers, and has complexity O{exp[c(logn)^(1/3)(loglogn)^(2/3)]}, (1) reducing the exponent over the continued fraction factorization algorithm and quadratic sieve. There are three values of c relevant to different flavors of the method (Pomerance 1996). For the "special" case of the algorithm applied to numbers...

  • Open Graph Meta Tags

    5
    • og:image
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_NumberFieldSieve.png
    • og:url
      https://mathworld.wolfram.com/NumberFieldSieve.html
    • og:type
      website
    • og:title
      Number Field Sieve -- from Wolfram MathWorld
    • og:description
      An extremely fast factorization method developed by Pollard which was used to factor the RSA-130 number. This method is the most powerful known for factoring general numbers, and has complexity O{exp[c(logn)^(1/3)(loglogn)^(2/3)]}, (1) reducing the exponent over the continued fraction factorization algorithm and quadratic sieve. There are three values of c relevant to different flavors of the method (Pomerance 1996). For the "special" case of the algorithm applied to numbers...

  • Twitter Meta Tags

    5
    • twitter:card
      summary_large_image
    • twitter:site
      @WolframResearch
    • twitter:title
      Number Field Sieve -- from Wolfram MathWorld
    • twitter:description
      An extremely fast factorization method developed by Pollard which was used to factor the RSA-130 number. This method is the most powerful known for factoring general numbers, and has complexity O{exp[c(logn)^(1/3)(loglogn)^(2/3)]}, (1) reducing the exponent over the continued fraction factorization algorithm and quadratic sieve. There are three values of c relevant to different flavors of the method (Pomerance 1996). For the "special" case of the algorithm applied to numbers...
    • twitter:image:src
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_NumberFieldSieve.png

  • Link Tags

    4
    • canonical
      https://mathworld.wolfram.com/NumberFieldSieve.html
    • preload
      //www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
    • stylesheet
      /css/styles.css
    • stylesheet
      /common/js/c2c/1.0/WolframC2CGui.css.en

Links

44