
mathworld.wolfram.com/PerfectPower.html
Preview meta tags from the mathworld.wolfram.com website.
Linked Hostnames
6- 32 links tomathworld.wolfram.com
- 5 links tooeis.org
- 4 links towww.wolfram.com
- 4 links towww.wolframalpha.com
- 3 links towww.amazon.com
- 1 link towolframalpha.com
Thumbnail
Search Engine Appearance
Perfect Power -- from Wolfram MathWorld
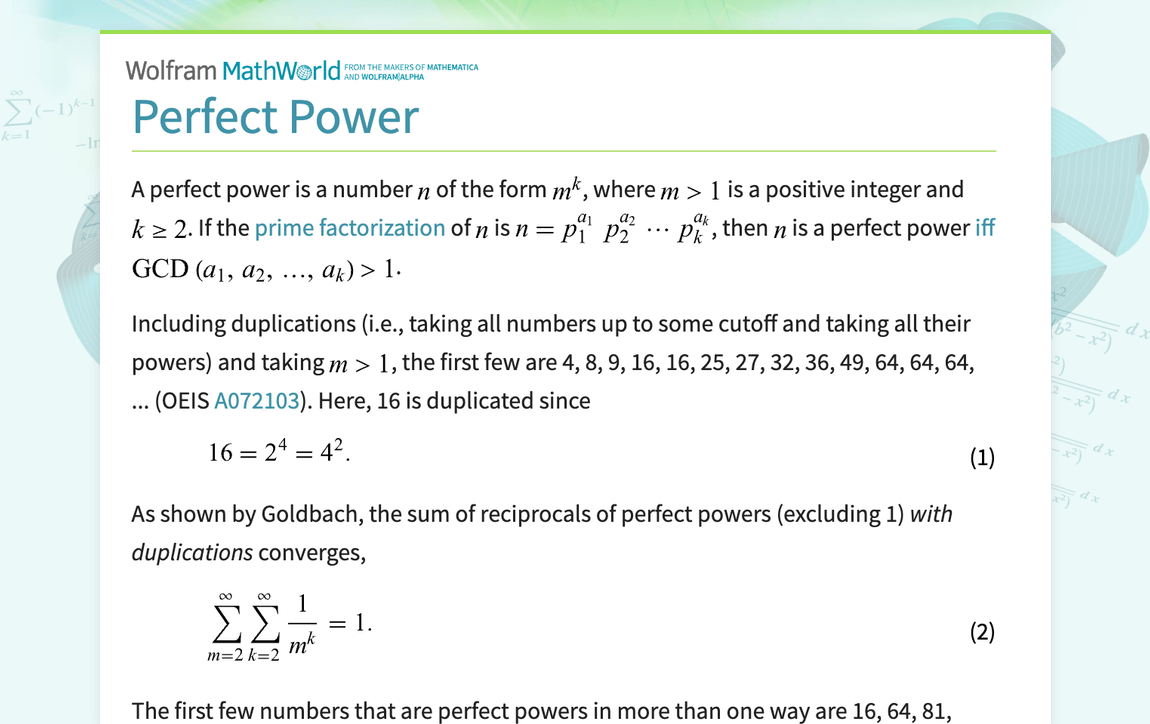
A perfect power is a number n of the form m^k, where m>1 is a positive integer and k>=2. If the prime factorization of n is n=p_1^(a_1)p_2^(a_2)...p_k^(a_k), then n is a perfect power iff GCD(a_1,a_2,...,a_k)>1. Including duplications (i.e., taking all numbers up to some cutoff and taking all their powers) and taking m>1, the first few are 4, 8, 9, 16, 16, 25, 27, 32, 36, 49, 64, 64, 64, ... (OEIS A072103). Here, 16 is duplicated since 16=2^4=4^2. (1) As shown by Goldbach,...
Bing
Perfect Power -- from Wolfram MathWorld
A perfect power is a number n of the form m^k, where m>1 is a positive integer and k>=2. If the prime factorization of n is n=p_1^(a_1)p_2^(a_2)...p_k^(a_k), then n is a perfect power iff GCD(a_1,a_2,...,a_k)>1. Including duplications (i.e., taking all numbers up to some cutoff and taking all their powers) and taking m>1, the first few are 4, 8, 9, 16, 16, 25, 27, 32, 36, 49, 64, 64, 64, ... (OEIS A072103). Here, 16 is duplicated since 16=2^4=4^2. (1) As shown by Goldbach,...
DuckDuckGo
Perfect Power -- from Wolfram MathWorld
A perfect power is a number n of the form m^k, where m>1 is a positive integer and k>=2. If the prime factorization of n is n=p_1^(a_1)p_2^(a_2)...p_k^(a_k), then n is a perfect power iff GCD(a_1,a_2,...,a_k)>1. Including duplications (i.e., taking all numbers up to some cutoff and taking all their powers) and taking m>1, the first few are 4, 8, 9, 16, 16, 25, 27, 32, 36, 49, 64, 64, 64, ... (OEIS A072103). Here, 16 is duplicated since 16=2^4=4^2. (1) As shown by Goldbach,...
General Meta Tags
23- titlePerfect Power -- from Wolfram MathWorld
- DC.TitlePerfect Power
- DC.CreatorWeisstein, Eric W.
- DC.DescriptionA perfect power is a number n of the form m^k, where m>1 is a positive integer and k>=2. If the prime factorization of n is n=p_1^(a_1)p_2^(a_2)...p_k^(a_k), then n is a perfect power iff GCD(a_1,a_2,...,a_k)>1. Including duplications (i.e., taking all numbers up to some cutoff and taking all their powers) and taking m>1, the first few are 4, 8, 9, 16, 16, 25, 27, 32, 36, 49, 64, 64, 64, ... (OEIS A072103). Here, 16 is duplicated since 16=2^4=4^2. (1) As shown by Goldbach,...
- descriptionA perfect power is a number n of the form m^k, where m>1 is a positive integer and k>=2. If the prime factorization of n is n=p_1^(a_1)p_2^(a_2)...p_k^(a_k), then n is a perfect power iff GCD(a_1,a_2,...,a_k)>1. Including duplications (i.e., taking all numbers up to some cutoff and taking all their powers) and taking m>1, the first few are 4, 8, 9, 16, 16, 25, 27, 32, 36, 49, 64, 64, 64, ... (OEIS A072103). Here, 16 is duplicated since 16=2^4=4^2. (1) As shown by Goldbach,...
Open Graph Meta Tags
5- og:imagehttps://mathworld.wolfram.com/images/socialmedia/share/ogimage_PerfectPower.png
- og:urlhttps://mathworld.wolfram.com/PerfectPower.html
- og:typewebsite
- og:titlePerfect Power -- from Wolfram MathWorld
- og:descriptionA perfect power is a number n of the form m^k, where m>1 is a positive integer and k>=2. If the prime factorization of n is n=p_1^(a_1)p_2^(a_2)...p_k^(a_k), then n is a perfect power iff GCD(a_1,a_2,...,a_k)>1. Including duplications (i.e., taking all numbers up to some cutoff and taking all their powers) and taking m>1, the first few are 4, 8, 9, 16, 16, 25, 27, 32, 36, 49, 64, 64, 64, ... (OEIS A072103). Here, 16 is duplicated since 16=2^4=4^2. (1) As shown by Goldbach,...
Twitter Meta Tags
5- twitter:cardsummary_large_image
- twitter:site@WolframResearch
- twitter:titlePerfect Power -- from Wolfram MathWorld
- twitter:descriptionA perfect power is a number n of the form m^k, where m>1 is a positive integer and k>=2. If the prime factorization of n is n=p_1^(a_1)p_2^(a_2)...p_k^(a_k), then n is a perfect power iff GCD(a_1,a_2,...,a_k)>1. Including duplications (i.e., taking all numbers up to some cutoff and taking all their powers) and taking m>1, the first few are 4, 8, 9, 16, 16, 25, 27, 32, 36, 49, 64, 64, 64, ... (OEIS A072103). Here, 16 is duplicated since 16=2^4=4^2. (1) As shown by Goldbach,...
- twitter:image:srchttps://mathworld.wolfram.com/images/socialmedia/share/ogimage_PerfectPower.png
Link Tags
4- canonicalhttps://mathworld.wolfram.com/PerfectPower.html
- preload//www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
- stylesheet/css/styles.css
- stylesheet/common/js/c2c/1.0/WolframC2CGui.css.en
Links
49- http://oeis.org/A001597
- http://oeis.org/A070428
- http://oeis.org/A072102
- http://oeis.org/A072103
- http://oeis.org/A117453