mathworld.wolfram.com/Power.html

Preview meta tags from the mathworld.wolfram.com website.

Linked Hostnames

8

Thumbnail

Search Engine Appearance

Google

https://mathworld.wolfram.com/Power.html

Power -- from Wolfram MathWorld

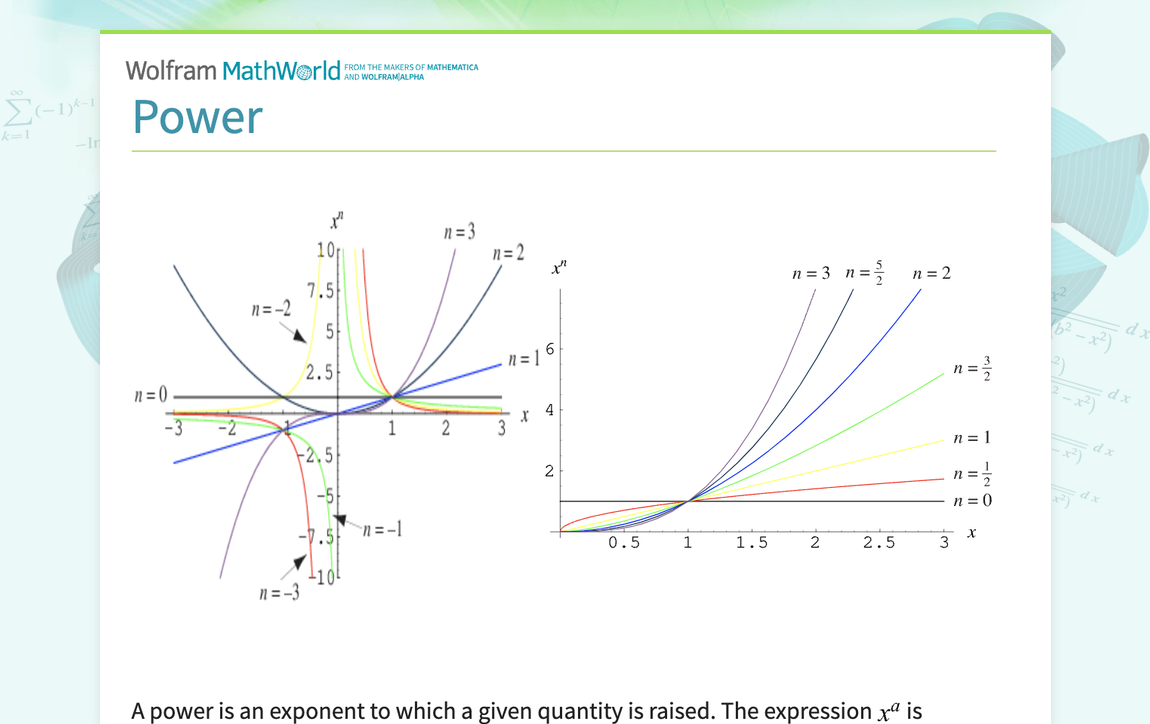
A power is an exponent to which a given quantity is raised. The expression x^a is therefore known as "x to the ath power." A number of powers of x are plotted above (cf. Derbyshire 2004, pp. 68 and 73). The power may be an integer, real number, or complex number. However, the power of a real number to a non-integer power is not necessarily itself a real number. For example, x^(1/2) is real only for x>=0. A number other than 0 taken to the power 0 is defined to be 1, which...



Bing

Power -- from Wolfram MathWorld

https://mathworld.wolfram.com/Power.html

A power is an exponent to which a given quantity is raised. The expression x^a is therefore known as "x to the ath power." A number of powers of x are plotted above (cf. Derbyshire 2004, pp. 68 and 73). The power may be an integer, real number, or complex number. However, the power of a real number to a non-integer power is not necessarily itself a real number. For example, x^(1/2) is real only for x>=0. A number other than 0 taken to the power 0 is defined to be 1, which...



DuckDuckGo

https://mathworld.wolfram.com/Power.html

Power -- from Wolfram MathWorld

A power is an exponent to which a given quantity is raised. The expression x^a is therefore known as "x to the ath power." A number of powers of x are plotted above (cf. Derbyshire 2004, pp. 68 and 73). The power may be an integer, real number, or complex number. However, the power of a real number to a non-integer power is not necessarily itself a real number. For example, x^(1/2) is real only for x>=0. A number other than 0 taken to the power 0 is defined to be 1, which...

  • General Meta Tags

    34
    • title
      Power -- from Wolfram MathWorld
    • DC.Title
      Power
    • DC.Creator
      Weisstein, Eric W.
    • DC.Description
      A power is an exponent to which a given quantity is raised. The expression x^a is therefore known as "x to the ath power." A number of powers of x are plotted above (cf. Derbyshire 2004, pp. 68 and 73). The power may be an integer, real number, or complex number. However, the power of a real number to a non-integer power is not necessarily itself a real number. For example, x^(1/2) is real only for x>=0. A number other than 0 taken to the power 0 is defined to be 1, which...
    • description
      A power is an exponent to which a given quantity is raised. The expression x^a is therefore known as "x to the ath power." A number of powers of x are plotted above (cf. Derbyshire 2004, pp. 68 and 73). The power may be an integer, real number, or complex number. However, the power of a real number to a non-integer power is not necessarily itself a real number. For example, x^(1/2) is real only for x>=0. A number other than 0 taken to the power 0 is defined to be 1, which...

  • Open Graph Meta Tags

    5
    • og:image
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_Power.png
    • og:url
      https://mathworld.wolfram.com/Power.html
    • og:type
      website
    • og:title
      Power -- from Wolfram MathWorld
    • og:description
      A power is an exponent to which a given quantity is raised. The expression x^a is therefore known as "x to the ath power." A number of powers of x are plotted above (cf. Derbyshire 2004, pp. 68 and 73). The power may be an integer, real number, or complex number. However, the power of a real number to a non-integer power is not necessarily itself a real number. For example, x^(1/2) is real only for x>=0. A number other than 0 taken to the power 0 is defined to be 1, which...

  • Twitter Meta Tags

    5
    • twitter:card
      summary_large_image
    • twitter:site
      @WolframResearch
    • twitter:title
      Power -- from Wolfram MathWorld
    • twitter:description
      A power is an exponent to which a given quantity is raised. The expression x^a is therefore known as "x to the ath power." A number of powers of x are plotted above (cf. Derbyshire 2004, pp. 68 and 73). The power may be an integer, real number, or complex number. However, the power of a real number to a non-integer power is not necessarily itself a real number. For example, x^(1/2) is real only for x>=0. A number other than 0 taken to the power 0 is defined to be 1, which...
    • twitter:image:src
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_Power.png

  • Link Tags

    4
    • canonical
      https://mathworld.wolfram.com/Power.html
    • preload
      //www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
    • stylesheet
      /css/styles.css
    • stylesheet
      /common/js/c2c/1.0/WolframC2CGui.css.en

Links

107