mathworld.wolfram.com/ReuleauxTriangle.html

Preview meta tags from the mathworld.wolfram.com website.

Linked Hostnames

13

Thumbnail

Search Engine Appearance

Google

https://mathworld.wolfram.com/ReuleauxTriangle.html

Reuleaux Triangle -- from Wolfram MathWorld

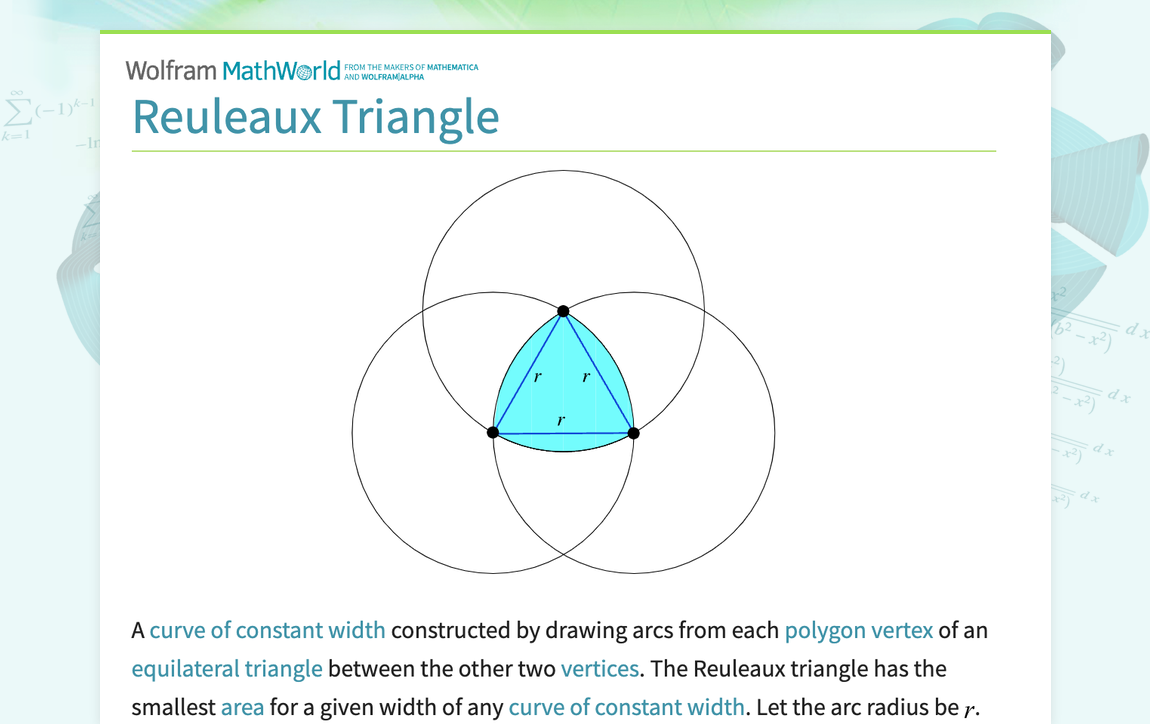
A curve of constant width constructed by drawing arcs from each polygon vertex of an equilateral triangle between the other two vertices. The Reuleaux triangle has the smallest area for a given width of any curve of constant width. Let the arc radius be r. Since the area of each meniscus-shaped portion of the Reuleaux triangle is a circular segment with opening angle theta=pi/3, A_s = 1/2r^2(theta-sintheta) (1) = (pi/6-(sqrt(3))/4)r^2. (2) But the area of the central equilateral...



Bing

Reuleaux Triangle -- from Wolfram MathWorld

https://mathworld.wolfram.com/ReuleauxTriangle.html

A curve of constant width constructed by drawing arcs from each polygon vertex of an equilateral triangle between the other two vertices. The Reuleaux triangle has the smallest area for a given width of any curve of constant width. Let the arc radius be r. Since the area of each meniscus-shaped portion of the Reuleaux triangle is a circular segment with opening angle theta=pi/3, A_s = 1/2r^2(theta-sintheta) (1) = (pi/6-(sqrt(3))/4)r^2. (2) But the area of the central equilateral...



DuckDuckGo

https://mathworld.wolfram.com/ReuleauxTriangle.html

Reuleaux Triangle -- from Wolfram MathWorld

A curve of constant width constructed by drawing arcs from each polygon vertex of an equilateral triangle between the other two vertices. The Reuleaux triangle has the smallest area for a given width of any curve of constant width. Let the arc radius be r. Since the area of each meniscus-shaped portion of the Reuleaux triangle is a circular segment with opening angle theta=pi/3, A_s = 1/2r^2(theta-sintheta) (1) = (pi/6-(sqrt(3))/4)r^2. (2) But the area of the central equilateral...

  • General Meta Tags

    19
    • title
      Reuleaux Triangle -- from Wolfram MathWorld
    • DC.Title
      Reuleaux Triangle
    • DC.Creator
      Weisstein, Eric W.
    • DC.Description
      A curve of constant width constructed by drawing arcs from each polygon vertex of an equilateral triangle between the other two vertices. The Reuleaux triangle has the smallest area for a given width of any curve of constant width. Let the arc radius be r. Since the area of each meniscus-shaped portion of the Reuleaux triangle is a circular segment with opening angle theta=pi/3, A_s = 1/2r^2(theta-sintheta) (1) = (pi/6-(sqrt(3))/4)r^2. (2) But the area of the central equilateral...
    • description
      A curve of constant width constructed by drawing arcs from each polygon vertex of an equilateral triangle between the other two vertices. The Reuleaux triangle has the smallest area for a given width of any curve of constant width. Let the arc radius be r. Since the area of each meniscus-shaped portion of the Reuleaux triangle is a circular segment with opening angle theta=pi/3, A_s = 1/2r^2(theta-sintheta) (1) = (pi/6-(sqrt(3))/4)r^2. (2) But the area of the central equilateral...

  • Open Graph Meta Tags

    5
    • og:image
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_ReuleauxTriangle.png
    • og:url
      https://mathworld.wolfram.com/ReuleauxTriangle.html
    • og:type
      website
    • og:title
      Reuleaux Triangle -- from Wolfram MathWorld
    • og:description
      A curve of constant width constructed by drawing arcs from each polygon vertex of an equilateral triangle between the other two vertices. The Reuleaux triangle has the smallest area for a given width of any curve of constant width. Let the arc radius be r. Since the area of each meniscus-shaped portion of the Reuleaux triangle is a circular segment with opening angle theta=pi/3, A_s = 1/2r^2(theta-sintheta) (1) = (pi/6-(sqrt(3))/4)r^2. (2) But the area of the central equilateral...

  • Twitter Meta Tags

    5
    • twitter:card
      summary_large_image
    • twitter:site
      @WolframResearch
    • twitter:title
      Reuleaux Triangle -- from Wolfram MathWorld
    • twitter:description
      A curve of constant width constructed by drawing arcs from each polygon vertex of an equilateral triangle between the other two vertices. The Reuleaux triangle has the smallest area for a given width of any curve of constant width. Let the arc radius be r. Since the area of each meniscus-shaped portion of the Reuleaux triangle is a circular segment with opening angle theta=pi/3, A_s = 1/2r^2(theta-sintheta) (1) = (pi/6-(sqrt(3))/4)r^2. (2) But the area of the central equilateral...
    • twitter:image:src
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_ReuleauxTriangle.png

  • Link Tags

    4
    • canonical
      https://mathworld.wolfram.com/ReuleauxTriangle.html
    • preload
      //www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
    • stylesheet
      /css/styles.css
    • stylesheet
      /common/js/c2c/1.0/WolframC2CGui.css.en

Links

75