mathworld.wolfram.com/SquareNumber.html

Preview meta tags from the mathworld.wolfram.com website.

Linked Hostnames

10

Thumbnail

Search Engine Appearance

Google

https://mathworld.wolfram.com/SquareNumber.html

Square Number -- from Wolfram MathWorld

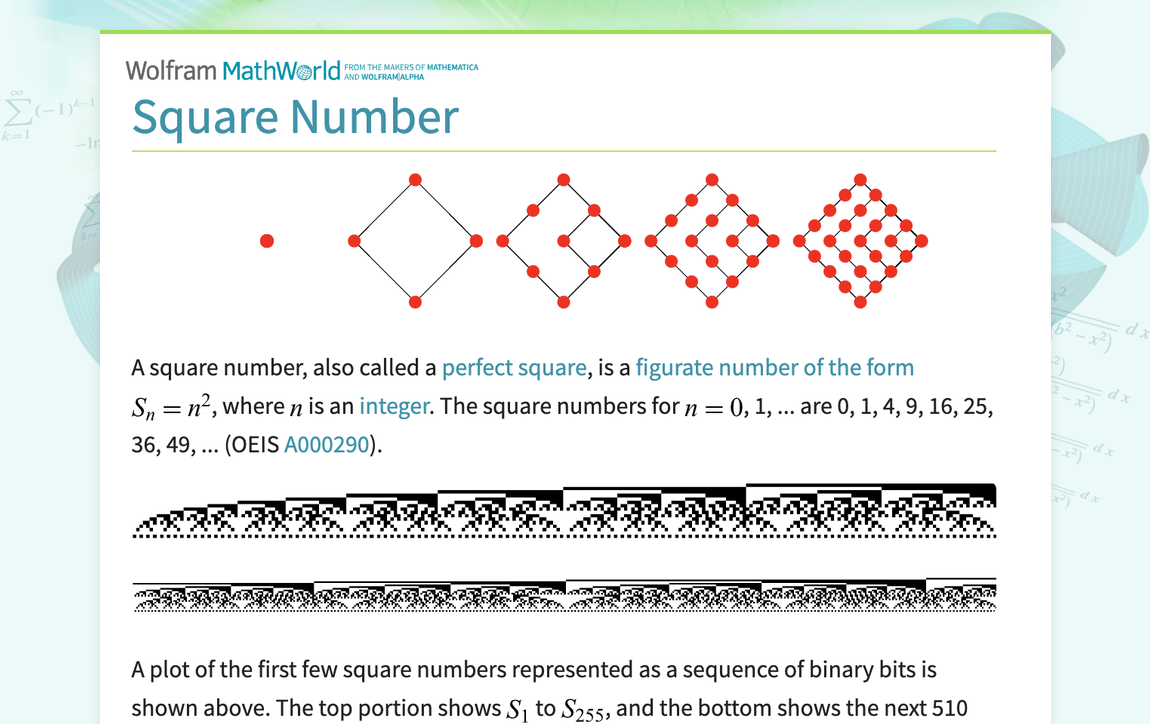
A square number, also called a perfect square, is a figurate number of the form S_n=n^2, where n is an integer. The square numbers for n=0, 1, ... are 0, 1, 4, 9, 16, 25, 36, 49, ... (OEIS A000290). A plot of the first few square numbers represented as a sequence of binary bits is shown above. The top portion shows S_1 to S_(255), and the bottom shows the next 510 values. The generating function giving the square numbers is (x(x+1))/((1-x)^3)=x+4x^2+9x^3+16x^4+.... (1) The (n+1)st...



Bing

Square Number -- from Wolfram MathWorld

https://mathworld.wolfram.com/SquareNumber.html

A square number, also called a perfect square, is a figurate number of the form S_n=n^2, where n is an integer. The square numbers for n=0, 1, ... are 0, 1, 4, 9, 16, 25, 36, 49, ... (OEIS A000290). A plot of the first few square numbers represented as a sequence of binary bits is shown above. The top portion shows S_1 to S_(255), and the bottom shows the next 510 values. The generating function giving the square numbers is (x(x+1))/((1-x)^3)=x+4x^2+9x^3+16x^4+.... (1) The (n+1)st...



DuckDuckGo

https://mathworld.wolfram.com/SquareNumber.html

Square Number -- from Wolfram MathWorld

A square number, also called a perfect square, is a figurate number of the form S_n=n^2, where n is an integer. The square numbers for n=0, 1, ... are 0, 1, 4, 9, 16, 25, 36, 49, ... (OEIS A000290). A plot of the first few square numbers represented as a sequence of binary bits is shown above. The top portion shows S_1 to S_(255), and the bottom shows the next 510 values. The generating function giving the square numbers is (x(x+1))/((1-x)^3)=x+4x^2+9x^3+16x^4+.... (1) The (n+1)st...

  • General Meta Tags

    27
    • title
      Square Number -- from Wolfram MathWorld
    • DC.Title
      Square Number
    • DC.Creator
      Weisstein, Eric W.
    • DC.Description
      A square number, also called a perfect square, is a figurate number of the form S_n=n^2, where n is an integer. The square numbers for n=0, 1, ... are 0, 1, 4, 9, 16, 25, 36, 49, ... (OEIS A000290). A plot of the first few square numbers represented as a sequence of binary bits is shown above. The top portion shows S_1 to S_(255), and the bottom shows the next 510 values. The generating function giving the square numbers is (x(x+1))/((1-x)^3)=x+4x^2+9x^3+16x^4+.... (1) The (n+1)st...
    • description
      A square number, also called a perfect square, is a figurate number of the form S_n=n^2, where n is an integer. The square numbers for n=0, 1, ... are 0, 1, 4, 9, 16, 25, 36, 49, ... (OEIS A000290). A plot of the first few square numbers represented as a sequence of binary bits is shown above. The top portion shows S_1 to S_(255), and the bottom shows the next 510 values. The generating function giving the square numbers is (x(x+1))/((1-x)^3)=x+4x^2+9x^3+16x^4+.... (1) The (n+1)st...

  • Open Graph Meta Tags

    5
    • og:image
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_SquareNumber.png
    • og:url
      https://mathworld.wolfram.com/SquareNumber.html
    • og:type
      website
    • og:title
      Square Number -- from Wolfram MathWorld
    • og:description
      A square number, also called a perfect square, is a figurate number of the form S_n=n^2, where n is an integer. The square numbers for n=0, 1, ... are 0, 1, 4, 9, 16, 25, 36, 49, ... (OEIS A000290). A plot of the first few square numbers represented as a sequence of binary bits is shown above. The top portion shows S_1 to S_(255), and the bottom shows the next 510 values. The generating function giving the square numbers is (x(x+1))/((1-x)^3)=x+4x^2+9x^3+16x^4+.... (1) The (n+1)st...

  • Twitter Meta Tags

    5
    • twitter:card
      summary_large_image
    • twitter:site
      @WolframResearch
    • twitter:title
      Square Number -- from Wolfram MathWorld
    • twitter:description
      A square number, also called a perfect square, is a figurate number of the form S_n=n^2, where n is an integer. The square numbers for n=0, 1, ... are 0, 1, 4, 9, 16, 25, 36, 49, ... (OEIS A000290). A plot of the first few square numbers represented as a sequence of binary bits is shown above. The top portion shows S_1 to S_(255), and the bottom shows the next 510 values. The generating function giving the square numbers is (x(x+1))/((1-x)^3)=x+4x^2+9x^3+16x^4+.... (1) The (n+1)st...
    • twitter:image:src
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_SquareNumber.png

  • Link Tags

    4
    • canonical
      https://mathworld.wolfram.com/SquareNumber.html
    • preload
      //www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
    • stylesheet
      /css/styles.css
    • stylesheet
      /common/js/c2c/1.0/WolframC2CGui.css.en

Links

160