mathworld.wolfram.com/HammersleyPointSet.html

Preview meta tags from the mathworld.wolfram.com website.

Linked Hostnames

5

Thumbnail

Search Engine Appearance

Google

https://mathworld.wolfram.com/HammersleyPointSet.html

Hammersley Point Set -- from Wolfram MathWorld

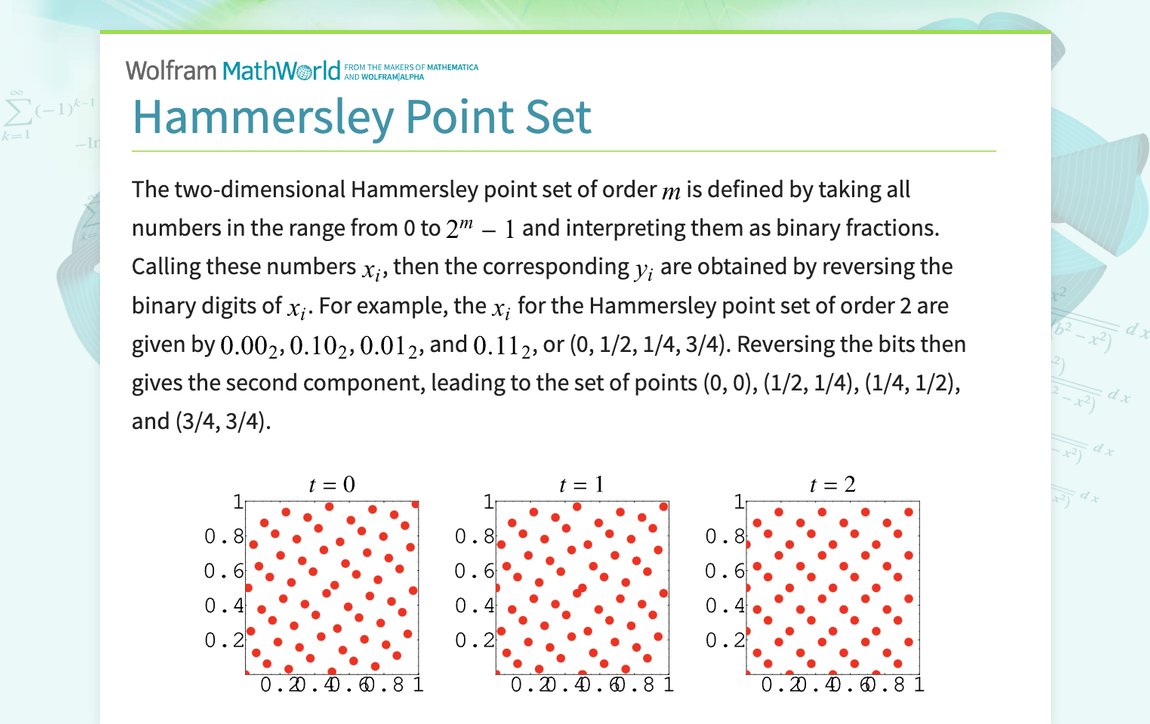
The two-dimensional Hammersley point set of order m is defined by taking all numbers in the range from 0 to 2^m-1 and interpreting them as binary fractions. Calling these numbers x_i, then the corresponding y_i are obtained by reversing the binary digits of x_i. For example, the x_i for the Hammersley point set of order 2 are given by 0.00_2, 0.10_2, 0.01_2, and 0.11_2, or (0, 1/2, 1/4, 3/4). Reversing the bits then gives the second component, leading to the set of points (0, 0), (1/2, 1/4),...



Bing

Hammersley Point Set -- from Wolfram MathWorld

https://mathworld.wolfram.com/HammersleyPointSet.html

The two-dimensional Hammersley point set of order m is defined by taking all numbers in the range from 0 to 2^m-1 and interpreting them as binary fractions. Calling these numbers x_i, then the corresponding y_i are obtained by reversing the binary digits of x_i. For example, the x_i for the Hammersley point set of order 2 are given by 0.00_2, 0.10_2, 0.01_2, and 0.11_2, or (0, 1/2, 1/4, 3/4). Reversing the bits then gives the second component, leading to the set of points (0, 0), (1/2, 1/4),...



DuckDuckGo

https://mathworld.wolfram.com/HammersleyPointSet.html

Hammersley Point Set -- from Wolfram MathWorld

The two-dimensional Hammersley point set of order m is defined by taking all numbers in the range from 0 to 2^m-1 and interpreting them as binary fractions. Calling these numbers x_i, then the corresponding y_i are obtained by reversing the binary digits of x_i. For example, the x_i for the Hammersley point set of order 2 are given by 0.00_2, 0.10_2, 0.01_2, and 0.11_2, or (0, 1/2, 1/4, 3/4). Reversing the bits then gives the second component, leading to the set of points (0, 0), (1/2, 1/4),...

  • General Meta Tags

    17
    • title
      Hammersley Point Set -- from Wolfram MathWorld
    • DC.Title
      Hammersley Point Set
    • DC.Creator
      Weisstein, Eric W.
    • DC.Description
      The two-dimensional Hammersley point set of order m is defined by taking all numbers in the range from 0 to 2^m-1 and interpreting them as binary fractions. Calling these numbers x_i, then the corresponding y_i are obtained by reversing the binary digits of x_i. For example, the x_i for the Hammersley point set of order 2 are given by 0.00_2, 0.10_2, 0.01_2, and 0.11_2, or (0, 1/2, 1/4, 3/4). Reversing the bits then gives the second component, leading to the set of points (0, 0), (1/2, 1/4),...
    • description
      The two-dimensional Hammersley point set of order m is defined by taking all numbers in the range from 0 to 2^m-1 and interpreting them as binary fractions. Calling these numbers x_i, then the corresponding y_i are obtained by reversing the binary digits of x_i. For example, the x_i for the Hammersley point set of order 2 are given by 0.00_2, 0.10_2, 0.01_2, and 0.11_2, or (0, 1/2, 1/4, 3/4). Reversing the bits then gives the second component, leading to the set of points (0, 0), (1/2, 1/4),...

  • Open Graph Meta Tags

    5
    • og:image
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_HammersleyPointSet.png
    • og:url
      https://mathworld.wolfram.com/HammersleyPointSet.html
    • og:type
      website
    • og:title
      Hammersley Point Set -- from Wolfram MathWorld
    • og:description
      The two-dimensional Hammersley point set of order m is defined by taking all numbers in the range from 0 to 2^m-1 and interpreting them as binary fractions. Calling these numbers x_i, then the corresponding y_i are obtained by reversing the binary digits of x_i. For example, the x_i for the Hammersley point set of order 2 are given by 0.00_2, 0.10_2, 0.01_2, and 0.11_2, or (0, 1/2, 1/4, 3/4). Reversing the bits then gives the second component, leading to the set of points (0, 0), (1/2, 1/4),...

  • Twitter Meta Tags

    5
    • twitter:card
      summary_large_image
    • twitter:site
      @WolframResearch
    • twitter:title
      Hammersley Point Set -- from Wolfram MathWorld
    • twitter:description
      The two-dimensional Hammersley point set of order m is defined by taking all numbers in the range from 0 to 2^m-1 and interpreting them as binary fractions. Calling these numbers x_i, then the corresponding y_i are obtained by reversing the binary digits of x_i. For example, the x_i for the Hammersley point set of order 2 are given by 0.00_2, 0.10_2, 0.01_2, and 0.11_2, or (0, 1/2, 1/4, 3/4). Reversing the bits then gives the second component, leading to the set of points (0, 0), (1/2, 1/4),...
    • twitter:image:src
      https://mathworld.wolfram.com/images/socialmedia/share/ogimage_HammersleyPointSet.png

  • Link Tags

    4
    • canonical
      https://mathworld.wolfram.com/HammersleyPointSet.html
    • preload
      //www.wolframcdn.com/fonts/source-sans-pro/1.0/global.css
    • stylesheet
      /css/styles.css
    • stylesheet
      /common/js/c2c/1.0/WolframC2CGui.css.en

Links

33